Turns out I have overlooked a module, the waveshaper.
Normally, I used it only for soft clip distortion. I never use it for my logic stuff because I always thought that the output never perfectly cancelled any unified DC offset due to smoothing and the CPU usage of the module was high.
However, I have realized that I was wrong, and this lead to a break through in Arithmetic and Logic Processing of SunVox. If you set the waveshaper into Mono LQ mode, you will now have a lookup table of 256 elements. Seems this is not much at the first glance, but this module redefines most of my understanding and the structures of Logic Processing in SunVox, which I thought it was impossible.
Take my integer to binary as an example:
To extract the binary of an number, you need to subtract a series of number in 2n and compare them individually.
This works reliably and I have used this structure for my VOXCOM and game of life, but I never thought about a simplification because I didn’t care about to use waveshaper due to the misconceptions.
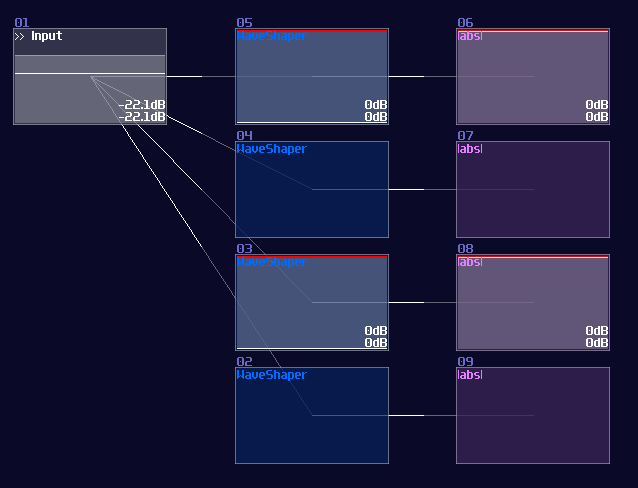
At this point, since I know the property of the LQ waveshaper, I found I have over complicated a logic structure that does simple stuff. I can basically use multiple waveshapers with a predefined curve to check either the value satisfied to the look up table.

With the aid of waveshapers, we can build something like so:
This design is more compact and is more efficient in CPU usage. There is a disadvantage though, which the new method has a much smaller operation range between 0 – 255, and it automatically shuts off in idle state. Despite the limitation, this is not really a issue since I prefer a channel of a module to represent a byte so that it is easier to build memories due to to limitations of distortion modules. (which has a bound)
This is just the tip of an iceberg, and we are not going to stop here yet. As some of the people know, we can use a pixilang generator to generate a curve for the waveshaper, but we never know that we can do precision mathematical calculation with that modules. Let me tell you about one of my SunVox problems and its solution.
I always thought instant division in SunVox was impossible, as we need to do multiple iterations of subtraction. Even if we have better ways like the Newton method, we still need to find a good estimation to get the correct result; otherwise, you still need to iterate as many times to get a great result.
This is no longer the case, and let me show you the equations and my solutions:
Inspired from a blog post by Paul Curtis, the newton method for division is xn+1 = x * ( 2 – a * x ), which a is the number you want to invert while x is the initial estimation.
Taking a = 3 and using x = 0.5 as an estimation. By applying the newton method a few times, you can easily to get a reasonable value of 1/3:
xn+1 = 0.5 * ( 2 – 3 * 0.5 ) = 0.25
xn+2 = 0.25 * ( 2 – 3 * 0.25 ) = 0.3125
xn+3 = 0.3125 * ( 2 – 3 * 0.3125 ) = 0.332031
xn+4 = 0.332031 * ( 2 – 3 * 0.332031 ) = 0.333328
In contrast, if you use a wrong estimation, not only you can’t get the correction value, but the value will also be unbounded (Let a = 5, and the estimation remains the same):
xn+1 = 0.5 * ( 2 – 5 * 0.5 ) = -0.25
xn+2 = -0.25 * ( 2 – 5 * -0.25 ) = -0.8125
xn+3 = -0.8125 * ( 2 – 5 * -0.8125) = -4.92578
xn+4 = -4.92578 * ( 2 – 5 * -4.92578 ) = -131.168
As you can see, -131 is certainly a wrong value to 1/5. No matter how many times you have iterated the function, you will never get 0.2.
I was puzzling about this problem because while the implementation from Paul Curtis is cool, this is not suitable for SunVox since bitwise operations in SunVox are expensive and SunVox is more efficient in processing parallelly than serially due to the modular environment. Until one day, I had discovered a simple hack to squarely get the estimation as best as SunVox can do, using the nearest 1/n for a. For example, we use 1/2 if a = 2, while we use 1/3 if a = 3, and so on.
People might argue that is not working because of the use of fraction, but here is where the waveshaper shines. Since we have a curve generator for the waveshaper which the curve generation is based on fraction, we can easily to generate a curve with the function of $y = 1 / n, so we can get a curve like this:

Problem solved; since we have a lookup table for the division result of the first 256 numbers, we can divide any 8bit integers in an O(1) manner; nevertheless, this isn’t even its final form, and let’s do a bit of calculation if x is not a whole number. Let a = 16.56 and finding the nearest integer divisor of 1/16.56 as estimation (0.0625 from 1/16):
xn+1 = 0.0625 * ( 2 – 16.56 * 0.0625 ) = 0.0603125
xn+2 = 0.0603125 * ( 2 – 16.56 * 0.0603125 ) = 0.0603863828125
xn+3 = 0.0603863828125 * ( 2 – 16.56 * 0.0603863828125) = 0.0603864734298157
xn+4 = 0.0603864734298157 * ( 2 – 16.56 * 0.0603864734298157) = 0.0603864734299517
Wait, what?! I can get a value of 1/16.56 with the precision after 15 decimal points! In fact, I only need three or four iterations to get a result that is so accurate for any application in SunVox. In addition, I have also discovered if we apply a division by 256 at the input and multiplication by 128 at the output, when the input signal is greater than 255, we can extend the range of the inverse function to any decimal numbers ranged between 1 – 65536. As a result, an ultimate solution for SunVox division has born:
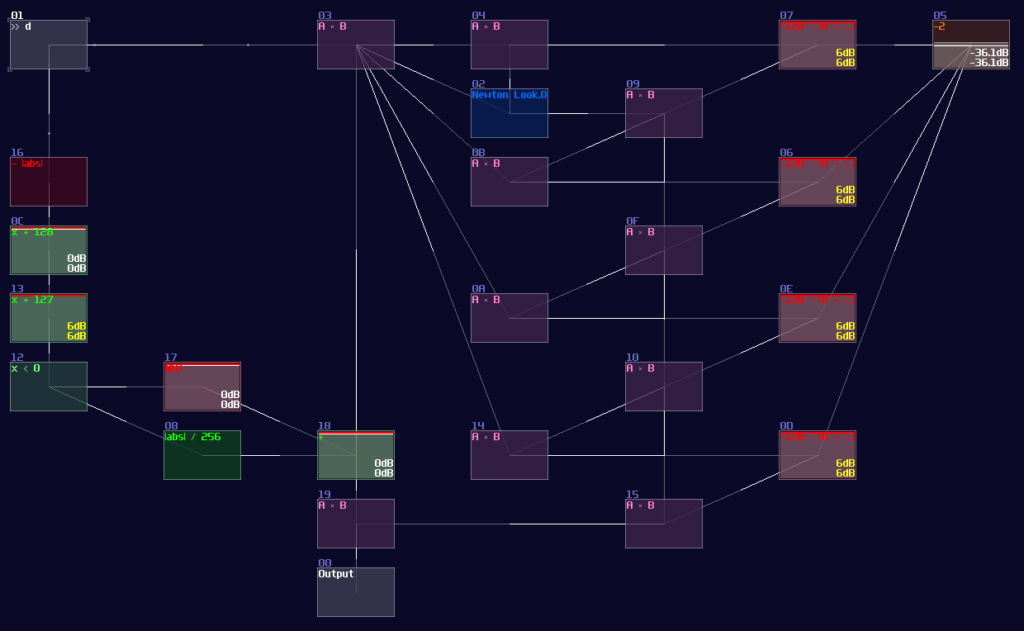
Now, we are finally able to solve one of the biggest challenges in SunVox. I will go through the application in 3xLog with other variant of division algorithms once I have completed other important chapters (and another amazing discoveries I didn’t tell you), along with the module, so you guys can use it out of the box without re-implementing the algorithm.
That’s about it, an overlooked module that changes the whole realm of SunVox logic! SunVox is a really cool software, you always find and learn something new even if you have been using it for so many years!
Soar beyond your imagination, and see you next time!